Right now, I am having a hard time understanding BGL’s (the Boost Graph Library) template spaghetti, so decided to write a blogpost while I decipher it, one at a time, documenting the whole thing along the way.

Day 1

Dmitry told me that I can most likely reuse the KisLazyFillGraph class in my astar search instead of trying to wrap KisPaintDevice to boost::graph since the former was already wrapped for the purpose of utilizing the graph algorithms that boost provide. Most of the code didn’t make any sense to me, but I will be optimistic and assume that by the end of the month, I would get hold of most of it. So let me ignore that for the moment will come back as I make some progress.

First Stop: The documentation of boost::astar_search of course. There are 3 kinds of boost::astar_search here, though I am yet to take a look at the source code, but I bet 2 of them just wrap the first one in some way. On a closer look, they have a lot of parameters, enough to scare any idiot like me. The versions which don’t initialize the maps (wild guess from the _no_init suffix) use an IncidenceGraph whereas the other versions use VertexListGraph. Looking at my heuristic function, I will probably need to use a VertexListGraph, since I need three points to calculate the cost, the previous point, the final point and the point in question.

Time to choose one of the interfaces to proceed further in the dissection, I am going with this one as the first choice, will try other if this didn’t work, reasons? use VertexListGraph, non named parameters and simpler than its sibling who also satisfies the first 2 reasons and I don’t think I would need VertexIndexMap or ColorMap but I might be wrong too.

template <typename VertexListGraph, typename AStarHeuristic,
          typename AStarVisitor, typename PredecessorMap,
          typename CostMap, typename DistanceMap,
          typename WeightMap,
          typename CompareFunction, typename CombineFunction,
          typename CostInf, typename CostZero>
inline void
astar_search_tree
  (const VertexListGraph &g,
   typename graph_traits<VertexListGraph>::vertex_descriptor s,
   AStarHeuristic h, AStarVisitor vis,
   PredecessorMap predecessor, CostMap cost,
   DistanceMap distance, WeightMap weight,
   CompareFunction compare, CombineFunction combine,
   CostInf inf, CostZero zero);

Parameters which matter:

AStarHeuristic: Interface for the heuristic function
AStarVisitor: Interface for the visitor
PredecessorMap: Vertex to Vertex mapping.
CostMap : Cost calculated at each vertex by the heuristic function? I guess
DistanceMap : Vertex to Distance mapping.
WeightMap: Seems similar to DistanceMap, to be fair I can’t tell.
CompareFunction : No idea, there is no page describing it.
CombineFunction : Same for this one.
CostInf: Okay, probably the maximum cost assigned before a vertex is discovered.
CostZero : Opposite of ConstInf I guess

Coming from Qt, boost has one of the horrible documentation to reckon with, it might be that I am looking at the wrong place, but well at least having some color scheme for the code doesn’t hurt, if not the broken/missing links. That should be enough for the day.

Day 2

Probably the choice I made yesterday of which interface to choose from was wrong, so going with the named parameter interface, today.

template <typename VertexListGraph,
          typename AStarHeuristic,
          typename P, typename T, typename R>
void
astar_search
  (const VertexListGraph &g,
   typename graph_traits<VertexListGraph>::vertex_descriptor s,
   AStarHeuristic h, const bgl_named_params<P, T, R>& params);

What is the that bgl_named_params<P, T, R> ? A little bit of toing and froing around the web, I found out the docs, voila, guess what, it is just template magic, here is an example from the docs.

bool r = boost::bellman_ford_shortest_paths(g, int(N), 
    boost::weight_map(weight). //Notice the period
    distance_map(&distance[0]). //It is here too
    predecessor_map(&parent[0]));

Not enough to deduce what should I put into the boost::astar_search, probably have to look at an example of boost::astar_search. I hope whatever the search engine has pointed me to as an example, is up-to-date with the latest versions.

The most important part of that example is the call to the boost::astar_search function,

astar_search(m_barrier_grid, s, heuristic,
    boost::weight_map(weight).
    predecessor_map(pred_pmap).
    distance_map(dist_pmap).
    visitor(visitor) );

What do those arguments mean?, lets follow the symbols,

boost::weight_map(weight)

Okay, following the variable weight, it is declared like,

boost::static_property_map<distance> weight(1);

Trusting every ounce of the boost documentation, boost::static_property_map says, “This property map wraps a copy of some particular object, and returns a copy of that object whenever a key object is input", thats easy, no fancy mutation magic of course. And that distance type is just a facade,

typedef double distance;

predecessor_map(pred_pmap)

Following pred_pmap,

typedef boost::unordered_map<vertex_descriptor,
                               vertex_descriptor,
                               vertex_hash> pred_map;
pred_map predecessor;
boost::associative_property_map<pred_map> pred_pmap(predecessor);

boost-confusion

Documentation of boost::associative_property_map please,

“This property map is an adaptor that converts any type that is a model of both Pair Associative Container and Unique Associative Container such as std::map into a mutable Lvalue Property Map. Note that the adaptor only retains a reference to the container, so the lifetime of the container must encompass the use of the adaptor.”

Okay, in short mutation magic for maps, which we can see as it takes in a boost::unordered_map and maps a vertex to another vertex, and that vertex_hash is just a hash function for the vertices,

struct vertex_hash:std::unary_function<vertex_descriptor, std::size_t> {
  std::size_t operator()(vertex_descriptor const& u) const {
    std::size_t seed = 0;
    boost::hash_combine(seed, u[0]);
    boost::hash_combine(seed, u[1]);
    return seed;
  }
};

distance_map(dist_pmap)

typedef boost::unordered_map<vertex_descriptor,
                             distance,
                             vertex_hash> dist_map;
dist_map distance;
boost::associative_property_map<dist_map> dist_pmap(distance);

Similar to the previous one, but this time instead of mapping to vertices to other vertices, it is now mapping distance to vertices, easy-peasy.

visitor(visitor)

Something new, following visitor, we get

astar_goal_visitor visitor(g);

What is that astar_goal_visitor ?

struct astar_goal_visitor:public boost::default_astar_visitor {
  astar_goal_visitor(vertex_descriptor goal):m_goal(goal) {};

  void examine_vertex(vertex_descriptor u, const filtered_grid&) {
    if (u == m_goal)
      throw found_goal();
  }

private:
  vertex_descriptor m_goal;
};

Ahh it just throws an exception whenever it finds the goal, okay, nothing much interesting here and g is the goal or the final vertex.

I would say I am a little bit confident now, but there are chances that I am going in the wrong direction, with that being said, I think it should be enough for Day 2.

Day 3

Last day, I dissected the bgl_name_params, today, one more interesting thing to dissect will be the heuristic function, which would be used to have a guess on which vertex is nearer to the goal and perform a better search.

astar_search(m_barrier_grid, s, heuristic,
    boost::weight_map(weight).
    predecessor_map(pred_pmap).
    distance_map(dist_pmap).
    visitor(visitor) );

heuristic

euclidean_heuristic heuristic(g);

And then,

class euclidean_heuristic:
      public boost::astar_heuristic<filtered_grid, double>
{
public:
  euclidean_heuristic(vertex_descriptor goal):m_goal(goal) {};

  double operator()(vertex_descriptor v) {
    return sqrt(pow(double(m_goal[0] - v[0]), 2) + pow(double(m_goal[1] - v[1]), 2));
  }

private:
  vertex_descriptor m_goal;
};

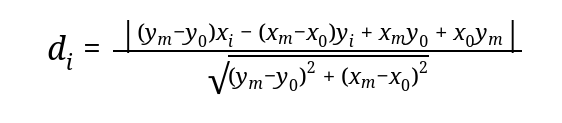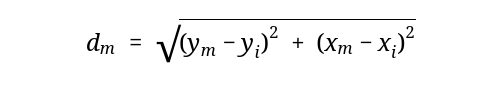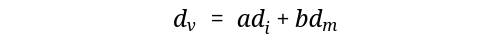First lets take a look at my proposed heuristic function, heuristic1 The m-suffixed variables are part of the final point, while the 0-suffixed one is for the previous point and the i-suffixed ones are of the current point. Calculates the deviation from the base line. heuristic2 Simple euclidean distance from the final point. heuristic3 This one combines them both, with coefficients a and b, which is to be determined experimentally. 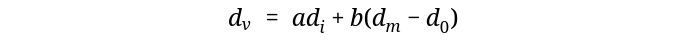Now that I think of it, we can further improove the equation by subtracting the distance of the previous point from the goal from dm, ending up with something like, heuristic4

I would be needing the previous vertex, the final vertex and the current vertex. The final and the current are obvious from the example, but not sure about the previous one. My wild guess, I should be using the predecessor_map and be done with it. Now if I modify the example function for the above equations,

class euclidean_heuristic:
      public boost::astar_heuristic<filtered_grid, double>
{
public:
  euclidean_heuristic(vertex_descriptor goal, 
                      boost::associative_property_map<pred_map> pmap):
          m_goal(goal), m_pmap(pmap), a(0.5), b(0.5) //experimental
          { }

  double operator()(vertex_descriptor v) {
    auto prev = m_pmap[v];
    auto di = (m_goal[1] - prev[1]) * v[0] + (m_goal[0] - prev[0]) * v[1];
    di = std::abs(di + prev[0] * m_goal[1] + prev[1] * m_goal[0]);
    auto dz = std::sqrt(std::pow(m_goal[1]-pred[1],2)+std::pow(m_goal[0]-pred[0],2));
    di = di/dz;
    auto dm = std::sqrt(std::pow(m_goal[1]-v[1],2)+std::pow(m_goal[0]-v[0],2));
    
    return a * di + b * (dm - dz);
  }

private:
  vertex_descriptor m_goal;
  boost::associative_property_map<pred_map> m_pmap;
  double a,b;
};

That should be enough for now, probably I can implement simply like this, but it surely requires some more research, which would be for some other blogpost. So, it is a :wq for today.

Dissecting boost::astar_search